First off, a disclaimer: I’ve never been good at math, or at least, not since the sixth grade or thereabouts. I’ve struggled with it enough that I suspect there’s something fundamental that I missed, or a mental block or even something about my brain (could be that root beer incident when I was 10,) but so what who cares? The point is, someone may be inclined to say that this explains my occasional antagonism towards certain aspects of math, and they might be right; I’d prefer to see someone outlining the flaws in my arguments, to be honest, rather than offering a dismissive assumption.
The next bit is a reflection of shortcuts in our thinking processes. I constantly caution against the human trait of taking cues from others and assuming they know what they’re talking about rather than applying our own reasoning, but there’s the recognition that any individual cannot possibly learn everything, so to a certain extent we have to take someone’s word for it. When it comes to the sciences, there are several things which give me pause, but I take the shortcut that scientists that are using these concepts on a daily basis have had plenty of time to catch the flaws that I might think I see, so first, I provisionally assume that it’s solid, but more importantly, I try to find out the details behind what has me stymied. This particular case, however, is a curious one, since it appears there is no firm agreement on many aspects of it, which is not a good sign. After a ridiculous amount of research and, really, more fucking around than should ever have to be spent on anything called a “theory,” I have finally arrived at my own views on the topic; whether you find these warranted is yet to be seen.
Part of this post is a book review, but only part, before we’ll move on to more pertinent aspects of the topic, which is chaos theory. In trying to find out more about this ‘theory,’ I stumbled across the book Chaos: Making a New Science, by James Gleick, a hefty tome that appeared well-illustrated and bore the enthusiastic testimonials of many, and figured this was a better place to start than the crowd-sourced and usually vague Wikipedia. The problem with this approach is that it permits only one perspective, and for some subjects this is not going to provide the best overview.
To be honest, I never finished the book – it was that bad. Not from the standpoint of grammar or sentence structure (like I could inform anyone on that,) but from the standpoint of being explanatory, informative, and even objective. I’ll elaborate on this shortly, but first, let’s pin down the topic itself a little better.
No matter what circles you move within, chances are you’ve at least heard of chaos theory. In and of itself it’s kind of hard to explain – It’s not exactly chaos as we normally use the word, meaning random and wildly variable, but instead a tendency to depart from expected results in an increasing manner; the phrase often associated with this diversion is “non-linear.” The gist is, within any kind of dynamic system (say air or water masses,) a very small variable can cause radical changes to ripple through the entire system; the example often used is that the flapping of a butterfly’s wings could potentially cause a hurricane thousands of kilometers away. In deterministic physics, this is not at all surprising, since any molecular interaction stands the very high potential of spreading among neighbors, and in fact everything is this big dance of interaction. Somehow, though, chaos is often claimed to disprove the tenets of determinism, radically so to hear Gleick and others tell it.
The second aspect of chaos is fractalism, where the pattern of the whole can be found, repeatedly, within the parts, going smaller and smaller. Or vice versa: start with a simple pattern and the pattern will grow by repeating itself. If you are having trouble reconciling this with the bit above, good – we’re on the same wavelength. And I have yet to find a source which has explained the connection; believe me, I’ve looked. At 317 pages one would think that Gleick’s book could manage to pin down the origin relatively quickly and move on to a detailed examination, but when I found myself halfway through the book and no clearer on the relation, or even the entire concept of chaos, I finally gave up hope for this to be explained in any way.
But the book was exemplary in illustrating one of the basic points of mathematics that I’ve had to repeat, which is that it is only an abstract, and its application to real-world situations has to take place with a certain level of fudging. Even as he presented example scenarios meant only to illustrate the effects of chaos, Gleick failed to provide anything that actually made sense. We’ll take his early example of mapping a shoreline, meant to demonstrate how this fractalism manifested. From a typical mapping distance, dozens to hundreds of kilometers above the surface, a shoreline is a meandering, random thing – but the closer you get to it, you’ll find that it remains random and meandering, and that at no level does it default to anything else. Now, as an example of fractal patterns, you might be excused if you fail to see how this is supposed to work, since “random” is not a pattern – it’s the absence of it, by definition. Randomness on a small scale – say, where the water meets sand grains – propagates upwards in scale to delineate the shoreline as seen from space? Preposterous! Yeah, a moment’s thought makes this a rather unimpressive example, doesn’t it? But it gets worse as we consider any example of a shoreline, perhaps where the cliffs erode into rocks and such like that. Get close enough, and you find the smooth surfaces of individual rocks, and closer still you find the crystalline structure of the same – but this pattern (the true meaning of the word now) doesn’t propagate very far at all; not even to naked eye level. And in fact, I have found no example of such fractalism anywhere in nature; it exists solely in mathematical realms. Sure, patterns of leaf veins or flower seeds may maintain a pattern very briefly, but such patterns do not, for instance, repeat even throughout the entire organism, nor can they be found at the microscopic level, much less the molecular one. So, where is this fractalism manifesting? Mind you, these are the examples of ‘real world’ fractalism, which says nothing of the wholly abstract and application-free examples such as computer-drawn Mandelbrot patterns and infinitely increasing the surface area of a cube by repeatedly cutting channels through each face (and each new one resulting from this practice.)
But let’s leave fractals behind and return to the more direct meaning of chaos theory. It’s easy to see how it might work with many different realistic scenarios, such as following driving directions. Making a left instead of a right at any given point, or taking the third right instead of the fourth, will ultimately fail to get us to our destination of course, but depending on where in the process this takes place, it may deliver us to wildly variable locations. And as any role-playing gamer knows, one crummy dice roll can change the entire campaign. The essence of chaos theory is the heart of every alternate scenario for WWII ever imagined.
Yet, there’s this concept called determinism, which relies on the wild idea that the laws of physics are, well, laws – as in, something unbreakable. Given force A and angles B and C and surface friction D, the dice could only arrive at one outcome; they appear random to us only because we have no handy, immediate way of calculating the factors involved. The concept of random actually means a result that does not originate from a known physical effect, coming from… well, apparently nowhere. We have extremely limited examples of such, only at the quantum level, and they disappear by the time they reach the atomic level; they might even originate from physical laws that we simply haven’t discovered yet. Which means that randomness is either extremely limited in scope, or completely nonexistent.
[Yes, this means for us too, and I’ve tackled that idea many times before.]
An awful lot of people, some mathematicians among them, don’t understand determinism in this way, instead believing it means predictable. But for something to be predictable, we would have to grasp all of the factors that impinge on the outcome, which for a great many subjects is simply outside of our abilities (see the dice roll example, or indeed anything at all about weather or most fluids.) Not knowing which way air molecules may twist in the turbulent interaction between warmer and cooler masses does not, in any way, mean that this process is outside of physical laws, any more than not knowing what is inside a box means the contents could be magical.
This has direct bearing on chaos theory; in fact, it is crucial to the idea that the theory even exists. A theory, in scientific terms, is an explanation for known facts, the process that produces the result. As such, not only must a theory fit the evidence we already have, it must predict future results accurately as well. When we look at the weather, or the turbulence of airflow over an aircraft’s wings, the function of chaos theory would be to predict the behavior that, so far, we have been unable to predict.
Unfortunately, it doesn’t do this. After getting halfway through the book and finding nothing of any real application – no solid information of any kind, actually – I went looking for other sources to see how this ‘theory’ was even supposed to work. And found… nothing. Every example within the book was strictly mathematical with no connection to physical processes; some of them were so far from reality that I just stared at them in confusion. Outside of the book wasn’t any better, producing nothing that was clarifying or even promising – I certainly might have missed something in my searches, but when every source that turns up says, at best, that chaos theory might be used to predict aircraft turbulence or increase the accuracy of weather reports, well, I don’t think I can be accused of jumping to conclusions. Especially since the theory has been around for decades, and Gleick’s book since 1987. For perspective, I point out the changes that have occurred in communications, biology, and even cosmology from that date, and let those be viewed against the idea that chaos is “the making of a new science.”
So let’s return to reviewing the book, before we jump back again to chaos theory itself. I am going to simplify the book down to two primary aspects – really, there isn’t much else in there. Both of them are miserably corrupt.
The science. Gleick either had no grasp of even rudimentary physics, or chose to misrepresent it to make chaos theory sound astounding; it really doesn’t matter which. He broadly, and repeatedly, implies that all of science predicts matter to behave in a linear fashion – no randomness, no variations. It’s hard to even imagine anyone stupid enough to believe this, because a quick look around demonstrates that this is not the case, but perhaps Gleick is one of those that hasn’t grasped the meaning of determinism. When a pale yellow leaf falls on a dark road, this alters the solar energy and temperature of the air masses above the road, by a tiny fraction of course, but this is multiplied by thousand of square meters of asphalt and millions of leaves even in a small geographic area; naturally, these ‘random’ alterations are capable of skewing a nice linear progression. Factors like this are what makes weather impossible to pin down – and yet, no part of this changes what we know about physics in any way.
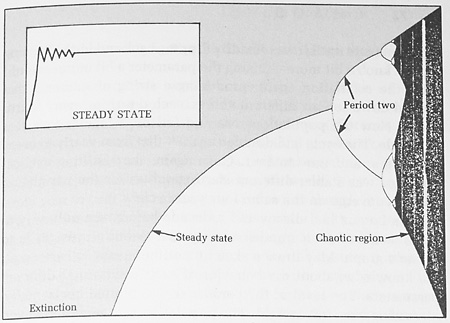
Now let’s look at Gleick’s specific example, using a simple math formula to plot virtual population growth. You can see that, at Period Two, the numbers split – but, how could they split? The population of this virtual species is both 750 and 1020 individuals? No, it would have to be bouncing between those two numbers on successive generations, so the line should zoom up and down between those points, not become two separate lines. But okay, let’s assume that some kind of ‘leveling’ algorithm is in use – such things are employed often to define a visible trend from a wildly disparate collection of plotted points. This still wouldn’t produce two sets of results unless someone purposefully began plotting two separate sets of numbers.
And then there’s the chaotic region, which demonstrates that no such algorithm is in use because any number of plots/figures would still average out to a single number. Worse still, we’re to believe, I suppose, that the population of these virtual animals [assigning random numbers because labeling a graph was too much effort] bounces back and forth between 61 and 12,482 individuals? I guess virtual animals can do this, but physical species would find that rather hard on the wombs…
Finally, there’s the very simple, but rather hard to ignore, factor that populations (as well as everything else in the real world) are affected by a hell of a lot more than a simple growth formula. There are real boom-and-bust scenarios in animal populations caused by disease, predation, surfeits of food, and so on, but no population ever reaches the point of chaos seen here, and in most cases present gradual changes and even fairly stable counts across many generations. So while running this formula presented a curious (if ridiculously illustrated) trend, it has no bearing whatsoever on what we might expect to see – or have ever seen. Even a situation such as bacteria in a culture dish, reducing the number of variable factors to an absolute minimum, is limited in range because reproduction can only take place at a certain rate, and crowding and food shortages will prevent too much of an increase. And this example isn’t alone: every demonstration of chaos in the half of the book that I read is just like this. So, is there even a possible scenario where a chaotic trend could be found? Gleick doesn’t say at all – that would have taken time away from:
The narrative. To hear Gleick tell it, the various mathematicians responsible for developing the concept of chaos were the most unappreciated and maligned people in our history of pursuing knowledge. The book is rife with how these souls struggled on against indifference and opposition, as dramatic as any 1950s screenwriter – in fact, reminding me irresistibly of the alt-med and cheap energy promotional screeds that can still be found; Gleick doesn’t come right out and say, “They all laughed…” but the tone is there nonetheless. And while I initially considered this drama and hyperbole, I eventually realized – at about the point where I stopped reading – that there may have been more of a grain of accuracy to this after all. There is no personality trait that can be applied to “scientists,” but the sciences have their own standards of publication and importance, which fosters a certain approach to new announcements. Essentially, one has to demonstrate both their rigor and the value of their ideas, most often in peer-reviewed journals. But esoteric mathematical formulas and properties will only gain attention from the ‘hard’ sciences if and when they can be used within those sciences. Had the population growth prediction above actually been seen in real-world population studies, chaos theory might have been vindicated; with a lot of examples, and/or some solid predictions of what would be found, chaos theory might be considered worthy of being called a “new science.” But when someone is just plugging numbers experimentally into a formula and finding anomalous and chaotic results, well, it could be an example of an emergent property in certain conditions, or it could be an example of an utterly worthless formula. The prudent thing to do is to figure this out first – but if it ever happened, Gleick didn’t see fit to include it.
This was, to me, the most annoying aspect of the book. While enthusiastic over the remarkable properties revealed within chaos theory, Gleick seemed unaware of what science is, or is intended to accomplish. Demonstrations, proofs, and even evidence were all somehow deemed unnecessary, and in their place the reader is expected to ride along with his awe of the theory; when Gleick did actually delve, ever so briefly, into actual physics, as often as not it would be with a degree of inaccuracy and misrepresentation, or with the complete ignorance that a lot of factors could impinge on any results. Even as he discusses moderately-high mathematical functions, seemingly aiming at an audience exceeding a high-school level of math knowledge, he fails to answer any of the questions that someone with a basic understanding of physics would ask; he either had no idea what his target audience is, or was aiming low while hoping to dazzle them with details they wouldn’t understand.
Now, let’s ditch the book and deal with chaos theory itself – and we’ll completely ignore the fractal aspect because I have yet to see any reason to even consider it. What that graph image above was intended to illustrate is how a simple formula could start to break down, vacillating between two sets of values, then two more, before further degrading into random values with no apparent pattern – this it the non-linear aspect of chaos, and something that we don’t expect math calculations to do. From a real-world physics standpoint, we see results such as this all the time, but that’s primarily because there are billions of factors that can come to bear on any given scenario; the lower the energy needed to effect a change, the more often it tends to occur. While a car sitting in a parking space will stay put (because the variations in energy that it absorbs from the sun and the wind and all that are too small to affect the collection of atoms bound together into a ‘piece,’) water molecules in a bucket move about and mix – a single drop of food coloring in an apparently-motionless bucket will still disperse, and given enough time it will spread evenly throughout all of the water rather than pooling at the bottom or going in a straight line anywhere. Thus, it is chaotic in nature, but hardly unexpected even when not specifically predictable. Physics is not in any way thwarted with this, and so it remains deterministic, even when the radiated body heat of someone leaning close to watch it affects the results in an infinitesimal manner.
But then there’s another aspect of chaos, and it is seen in that same illustration. At times, within the chaos region, the results can suddenly stabilize and follow a linear progression again briefly, shown by the clear areas in the middle of the scribbles. What magic is this?
Actually, no source that I have found has yet demonstrated that it’s not simple synchronicity. Take two different pieces of music with different tempos and play them simultaneously, and the beats will match at times – over a period of time (much longer than most pieces of music last) and the combined pieces will have a beat of their own, much slower than either of the originals, where the original beats match up. And getting similar results from a mathematical formula is hardly surprising, because a formula is a pattern. This is actually an issue in computing, because the nature of calculations means it is impossible to produce a truly random number when needed – if it originates from any previous function, then it is not random. Oh, it’s easy enough to produce something unpredictable for most functions, just like a die roll, but in critical applications where any induced pattern skews the results, such patterns cannot actually be escaped.
So, what is chaos? Is it truly random behavior, or simply unpredictable? If we’re using math to demonstrate it, it’s not random. If it’s unpredictable, then what purpose is it supposed to serve? We have plenty of unpredictable situations now – the value lies in changing them to predictable. Does that pattern illustrated above serve a purpose? Sure, if it can be shown to predict animal populations over time – but since it cannot factor in any of the billions of influences on such populations, it’s certainly not going to match any real world results in any way. So what part of this can even remotely be considered a science?
When I tossed the book aside and began searching for a better grasp of chaos theory, I came across numerous examples of the same kind of enthusiasm and promises that chaos would prove to be of great value – and I emphasize the ‘would’ because, even after decades, no one apparently had real examples of how it could be applied. I still wondered about what I was missing myself, because it seemed that so many higher-educated people couldn’t be so far off base about it – and then my friend Dan Palmer directed me to a webpage entitled, ‘What are the practical applications of chaos theory?‘ with this opening statement by Ted Pavlic, an Assistant Professor of Engineering, Sustainability, Physics, and Life Sciences:
Chaos theory isn’t something to be exploited for application. It doesn’t represent some mathematical or scientific discovery that can be used in novel ways. Instead, it represents a set of techniques for analyzing dynamical systems that are deterministic (i.e., they follow apparently simple rules that lead to behaviors which depend only upon their initial conditions) and yet very sensitive to perturbations of input. Consequently, advances in understanding certain classes of these systems lead to advances in either understanding the physical world or designing technology that interfaces with such systems.
…and, finally, some light began to dawn. Chaos theory is a demonstration that, in narrow circumstances, the basic mathematics of the situation may produce behavior that appears ‘random,’ (to be more specific, affected by other unknown factors) when it is actually just a pattern that emerges. When the numbers are departing from a nice linear or exponential progression, we would normally expect something else to be having an affect, but it might only be the way the numbers must behave in those circumstances.
You will note that Pavlic specifically includes determinism in his explanation, making it clear that chaos does not thwart or depart from the concept – something that Gleick at least inferred on multiple occasions. Far from being a new science, it is a refinement of expectations, one more factor that could have taken affect in the results. In most situations, that’s one out of thousands or perhaps millions of factors, and any of those that alter the numbers used in the equation will naturally affect the results from such. It’s easy to see that the circumstances where chaos theory becomes useful are very constrained.
I said above that there is no firm agreement on what chaos theory is and what it does, or can do, and this is reflected in the number of wildly disparate claims from various sources; Pavlic’s view is hardly representative of either the theory or those who promote it, including the author of this dismal and dismissable book. Yet, it was the only view that actually made any sense at all, or that showed a connection with any real-world scenarios in the slightest; note that Pavlic is not a mathematician, but a professor of physics and engineering. Also note that, as we go deeper into the very short explanation he provided, we yet again get into what chaos could do, but not what it does.
What I finally arrived at – and I will openly admit this is an opinion, and I couldn’t care less who takes issue with it – is that there are way too many people with a vested interest in making chaos theory something that it isn’t, somehow pertinent to the hard sciences as a whole rather than an occasional factor in extremely narrow circumstances. And this is perhaps not surprising; if you’ve chosen mathematics as a career, there really isn’t a lot of room for new discoveries – the vast majority of formulas and algorithms used in any hard science were established decades to centuries ago, making mathematics a function rather than any kind of research field. I can’t help but see chaos theory as a desperate attempt to appear relevant and groundbreaking in a field that offers virtually no opportunities for such recognition.
* * * *
Additional Reading:
Introduction to Chaos and it’s [sic] Real World Applications, by George T. Yurkon – Another link provided by Dan Palmer, this one gets to the point much faster than Gleick’s book, and demonstrates how deterministic physics can produce disparate results with only minimal changes in conditions, but still fails to recognize that a) we never actually see this take place, and b) just to produce the patterns shown within, there must be no other mitigating factors – something that simply doesn’t occur in real world applications. We’re just shy of 19 years since that paper was published, with bold promises of what chaos theory would produce, and I am still unable to find any solid results.